

We are going to create an application that allows the user to create expressions that evaluate to colors and then eventually to images. This may sound a little strange, but the results can be quite spectacular.
Here is the general idea: an image is really a expression that maps points (x,y) to colors (r,g,b). The application evaluates the expression for each pixel (x-, y-point) in the image and stores resulting color.
For this program, a color represents three real numbers, one each for the red, green and blue component, where the component values range from -1 to 1. For example, [-1,-1,-1] is black, [1,-1,-1] is red, and [1, 1,-1] is yellow. During computation of an expression, the value of each component should not be restricted to this range, but the final result of the expression should be clamped to within the range -1 to 1.
By default, like the colors, the domain of the image over X and Y
is from -1 to 1. The upper left corner of the image will be (-1,-1)
and the lower right corner will be (1, 1). Thus, the size of the image
will need to be mapped to the domain (in this case, [-1, 1]). Before
the expression is evaluated for each pixel, the
variables x and y should be set to the
current point to be evaluated.
Your program should allow a user to input expressions interactively or from a file and display the resulting image. The syntax of the allowed expressions is given below:
Note: If a function is scalar, i.e., typically operates on a single value (e.g., sin(x)), then it should be applied to each of the color components in turn.
| expression | syntax | semantics | examples |
|---|---|---|---|
| Constant | <any real number> [-]?[0-1]+(.[0-9]+)? |
a real valued number (note, to avoid potential ambiguity in parsing there should not be a space between the negative sign and the value) | .87 1 -0.4 |
| Color |
[ constant, constant, constant ] |
an RGB color where each value can be any constant |
[1, -1, 0.25] [0.5, 1, 1] |
| String | <any non-quote character between quotes> |
an image of the given file name is read, if the image cannot be read, an all black image is produced note, this should return the nearest color from the image at the current (x, y) values |
"foo.jpg" "images/mickey.gif" |
| Variable |
<any alpha-numeric string> [a-zA-z0-9]+ |
an expression represented by a word
note, two variables x and y should
always be defined to be the current coordinate in the image
domain
|
a
bugs q45 |
| Assignment | var = expr | assigns an expression to a variable |
a = 1.0 bugs = "foo.png" a = bugs |
| Unary Operator | op expr | prefixes an expression
! // negate (i.e., invert) a color |
!a !(t + a * 0.1) |
| Binary Operator | expr op expr | combines two expressions into a single
expression (in precedence order)
^ // exponentiate * // times / // divide + // plus - // minus |
a + b
a / 2 a + 1.0 * c |
| Unary Functions | fun(expr) | a function that takes an expression as its single argument
floor // round down ceil // round up abs // absolute value clamp // clamp results to [-1, 1] wrap // wrap results around [-1, 1] (i.e., 1.5 -> -0.5) sin // sine cos // cosine tan // tangent atan // arc tangent exp // e ^ parameter log // log -- use the absolute value of the parameter rgbToYCrCb // convert color to luminance / chrominance space yCrCbtoRGB // convert color to RGB from luminance / chrominance space |
sin(a * b)
abs(x) - y / 2 |
| Multi-Argument Functions | fun(expr,...) | a function that takes two or more expressions as its arguments
perlinColor(expr, expr) // create random color based on 2D noise perlinBW(expr, expr) // create grey scale color based on 2D noise // imports image, tiling it so it may be repeated imageWrap(string, x-coord-expr, y-coord-expr) // imports image, clipping it so it only appears once imageClip(string, x-coord-expr, y-coord-expr) // If you look at the example on the Intrinsics page, it includes an // arbitrary expression for x and y, so those may go out of the -1 to 1 // bounds you are using. Thus clip and wrap are two different // ways to guarantee those values passed to the image's f(x, y) function // are within the bounds. random() // returns random color (actually no arguments :) ) |
perlinColor(x, y) perlinBW(y, x+x) |
| Parentheses | (expr) | raises an expression's precedence | (a + b) * 3 !(bugs - 0.1) |
Operators have the following precedence (listed from highest to lowest):
| () | parentheses |
| ! | unary operators |
| ^ | exponentiation |
| *, /, % | multiplicative operators |
| +, - | additive operators |
| = | assignment |
For example, here are several images generated from basic expressions.
Note, not all of these functions are defined continuously. You should have appropriate error handling (e.g., divide-by-zero should silently return zero).
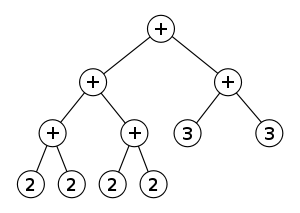
Expression Trees are trees in which the terminal nodes (leaves) represent variables or constants in an expression and the non-terminal (internal) nodes represent the operators. The inherent hierarchical nature of trees precisely capture operator precedence and provide a convenient mechanism for storing, traversing, and transforming expressions. Note, that unlike binary trees, each node of an Expression Trees can have any number of children, easily modeling operators with one, two, or even arbitrary numbers of arguments.
Expression Trees were first introduced in 1967 with the programming language LISP, in which the program itself is stored as an expression tree, called an s-expression, that can even be modified while the program is running! Since then, expression trees have formed the heart of many applications: representing genes, regular expressions, language grammars, and queries. They are so widespread that the World Wide Web Consortium (W3C) decided to use them as the core of the XML Document Object Model (DOM) specification, more than thirty years later!
Thus, the trickiest part about using expression trees is actually creating them from a given formatted input string. Parsing is the process of taking string organized by a grammatical structure (that defines key characters to act as separators between the characters that are important, e.g., whitespace or semi-colon characters in Java) and producing a list of tokens in an order that is easy to convert into an expression tree. During the parsing process, the important sequences of characters are converted into token objects, while the separators are typically thrown out. If the input string contains grammatical errors such that it cannot be parsed, then an error is reported.
Here is a standard algorithm to convert an infix expression into a postfix expression, which is then easy to convert into an Expression Tree.
Your application should be thoroughly tested to prove that your confidence in it is justified. You should include whatever data files, driver programs, or unit tests you have used (as well as documentation on how to use them, if appropriate).
There are many extensions to the basic specifications possible; some are listed below. The most important thing is that your program is designed well (i.e., there is a clear separation between the syntax and semantics of the expression language and that it is clearly possible to change by adding only O(1) line to your existing code). This means your design should be open to adding new kinds of expressions while closed to changing the evaluation and parsing code. The requirements above and suggestions below are intended to help you to realize such a design.
The extensions below are intended to stretch your design further and to differentiate your program from others to capture the algorithmic art market. Your team must extend the program beyond the core specifications given above for full credit. These extensions must further the good design of your program and not simply be hacks of code added at the last minute. If you do not have time to implement an extension, partial credit may be given for excellent justification of how your design either supports adding such a feature already or how it would need to changed sufficiently to support such a feature. Your design should support adding any of these features reasonably easily.
Your team will implement three extensions.
This project is worth 20% of your final grade.
This version should allow
The team will demo this program in class on Monday to the professor and discuss their design decisions.
Include documentation of extensions and how to use.
Tag this version in Subversion with the name final_implementation. This version should not have compiler errors. In Subclipse, look at Team --> Branch/Tag
Put the tagged version in the tags directory, rather than the trunk directory.
You can confirm that you did the above correctly by viewing the Subversion repository. Go to Window --> Show View --> SVN Repository Your repository should look something like this: 